In our day-to-day life, we use decimal numbers or integers as part of the base-ten numeral system. However, computers store information in bits that are made of 0s and 1s, this comprising the base-two numeral system.
In this article, I will explain how to convert decimals into binary numbers and vice versa. I will also detail how some of Python’s bitwise operations work, explaining how individual bits of data can be worked with at their most basic level.
In order to convert an integer into its binary form, we need to use exponents of 2, as shown in the table below. Let’s take a closer look at this process, using integer 75 as an example.
How do you convert the integer 75 into its binary form?Step 1: Find the largest number close to but smaller than 75 in the base-two numeral system, which is 64 (as shown in the table below).
Step 2: Subtract 64 from 75. This leaves us with 11.
Step 3: Repeat this same process until we reach 0.
a) Find the largest number close to but smaller than 11, which is 8. Then, subtract 8 from 11. This leaves us with 3.
b) Find the largest number close to but smaller than 3, which is 2. Then, subtract 2 from 3. This leaves us with 1.
c) Find the largest number close to 1, which is 1. Then, subtract 1 from 1. This leaves us with 0.
Step 4: Place 1 under all numbers we used, and 0 under all numbers we didn’t use. This way, we get binary number 1001011 for integer 75.

How do you convert 1001011 into its integer form?
Step 1: Place all binary numbers in the base-two table shown above.
Step 2: Add together all numbers that correspond with the 1s in binary. In this case: 64 + 8 + 2 + 1 = 75; we get 75.
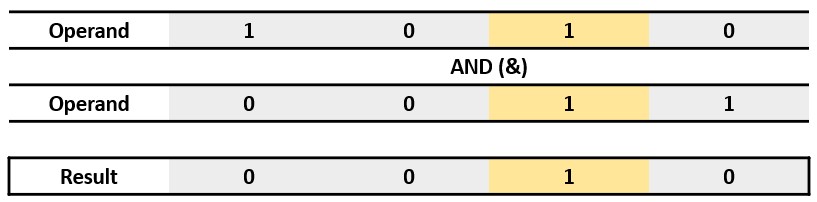
Bitwise AND (&)
When both bits are 1, it returns 1. Otherwise, it returns 0.
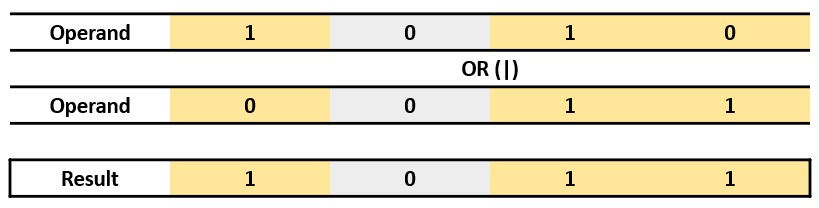
Bitwise OR (|)
As long as there is 1, it returns 1. Otherwise, it returns 0.
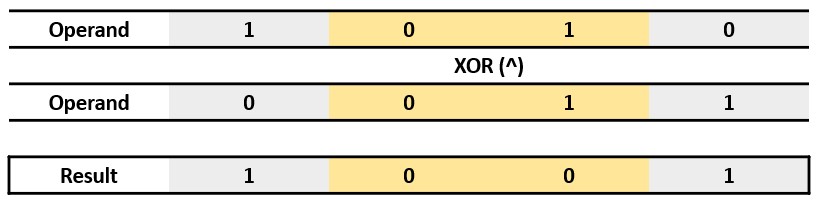
Bitwise XOR (^)
When both bits are the same, it returns 0. However, when both bits are different, it returns 1.
Bitwise NOT (~)
Bitwise NOT (~) switches each bit to its opposite (1s become 0s, and 0s become 1s). If the inverted number becomes negative, in order to store the negative number, we use the 2’s complement method. This can be done using the formula ~(a) = -(1+a). Let’s use the decimal 10 (binary 1010) as an example:
a = 1010 ~a = ~1010 ~a = -(1010 + 1) ~a = -(1011) ~a = -11 (Decimal)
Left Shift (<<)
The bitwise left shift operator << indicates that every bit should be shifted to the left by a specified number. In our example below, we left shift by one position. Shifting bits to the left by one position doubles its integer value. The leftmost bits always get dropped if there is a boundary and the rightmost bits are filled with 0.

Right Shift (>>)
The bitwise right shift operator >> indicates that every bit should be shifted to the right by a specified number. In our example below, we right shift by one position. Shifting bits to the right by one position halves its integer value. The rightmost bits always get dropped and the new leftmost bits are filled with 0 or 1 in case of a negative number.

Below is a list of practice problems from Leetcode about bit manipulation. I hope it helps you better understand how to conduct some of the more complex operations using bits.
https://leetcode.com/problems/single-number/
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ans = 0
for num in nums:
ans ^= num
return ans
https://leetcode.com/problems/reverse-bits/
class Solution:
def reverseBits(self, n: int) -> int:
ans = 0
for _ in range(32):
ans <<= 1
ans |= n & 1
n >>= 1
return ans
https://leetcode.com/problems/number-of-1-bits/
class Solution:
def hammingWeight(self, n: int) -> int:
cnt = 0
while n:
if n & 1 > 0:
cnt += 1
n >>= 1
return cnt
https://leetcode.com/problems/power-of-two/
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return n > 0 and n & (n-1) == 0
https://leetcode.com/problems/missing-number/
class Solution:
def missingNumber(self, nums: List[int]) -> int:
n = len(nums)
t = 0
for i in range(1, n + 1):
t ^= i
t ^= nums[i - 1]
return t
https://leetcode.com/problems/counting-bits/
class Solution:
def countBits(self, n: int) -> List[int]:
ans = [0] * (n + 1)
for i in range(1, n + 1):
ans[i] = ans[i >> 1] + (i & 1)
return ans
https://leetcode.com/problems/find-the-difference/
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
ans = 0
for c in s:
ans ^= ord(c)
for c in t:
ans ^= ord(c)
return chr(ans)
https://leetcode.com/problems/binary-watch/
class Solution:
def readBinaryWatch(self, turnedOn: int) -> List[str]:
ans = []
for i in range(12):
for j in range(60):
if (bin(i) + bin(j)).count('1') == turnedOn:
ans.append(str(i) + ':' + ('0' if j < 10 else '') + str(j))
return ans
https://leetcode.com/problems/hamming-distance/
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
cnt = 0
while x > 0 or y > 0:
if (x & 1) != (y & 1):
cnt += 1
x >>= 1
y >>= 1
return cnt
https://leetcode.com/problems/number-complement/
class Solution:
def findComplement(self, num: int) -> int:
p = 0
ans = 0
while num > 0:
ans += (1 - (num & 1)) * (2 ** p)
p += 1
num >>= 1
return ans
https://leetcode.com/problems/binary-number-with-alternating-bits/
class Solution:
def hasAlternatingBits(self, n: int) -> bool:
flag = n & 1
n >>= 1
while n > 0:
flag = 1 - flag
if (n & 1) != flag:
return False
n >>= 1
return True
https://leetcode.com/problems/xor-operation-in-an-array/
class Solution:
def xorOperation(self, n: int, start: int) -> int:
curSum = 0
for i in range(n):
curSum ^= start + 2 * i
return curSum
https://leetcode.com/problems/base-7/
class Solution:
def convertToBase7(self, num: int) -> str:
if num == 0:
return '0'
s = ''
n = abs(num)
while n > 0:
s += str(n % 7)
n //= 7
s = s[::-1]
return '-' + s if num < 0 else '' + s
https://leetcode.com/problems/convert-a-number-to-hexadecimal/
class Solution:
def toHex(self, num: int) -> str:
s = "0123456789abcdef"
ans = ""
if num == 0:
return "0"
elif num < 0:
num += 2**32
while num > 0:
ans += s[num % 16]
num >>= 4
return ans[::-1]